研究紹介
外場によって駆動されている非平衡量子系を主な舞台として、「新奇な量子相を実現するための物理系の設計」や「非平衡状態に特有な新しい物理現象の探求」といったテーマについて理論的な研究を行っています。
非摂動的な効果に起因する伝導現象
絶縁体や半導体といったエネルギーギャップを持った物質では、通常は電圧を印加しても電流が流れません。しかし、電場を強くしていくと量子力学的な効果(Landau-Zenerトンネリング)によって突然大きな電流が流れ始めることが知られています。
このトンネル効果が起こる確率は電場に関してTaylor展開できない関数形であることが知られており、電場強度に関する摂動展開がベースになっている従来の応答理論ではこの伝導現象が記述できません。我々は複素解析を応用した理論手法を用いることで、この非摂動的な効果に起因する伝導現象の従来にない新しい特徴を明らかにする研究を進めています。
幾何学効果による非相反トンネリング
電子は弱い電場のもとでは断熱的に運動します(断熱定理)。その意味で、強い電場のもとで起こるトンネリング現象は、断熱性の破綻ともみなすことができます。一方、電子の断熱運動には、物質のトポロジカルな応答の起源となる幾何学位相と呼ばれるものが顔を出します。
そこで我々はトンネリング現象への幾何学位相の寄与に着目した解析を行いました。すると、一般に空間反転対称性の破れた絶縁体においては、幾何学効果によってトンネル確率が非相反性を獲得すること、つまりは電圧の符号に応じて電流量が変化する整流性が現れることを明らかにしました。
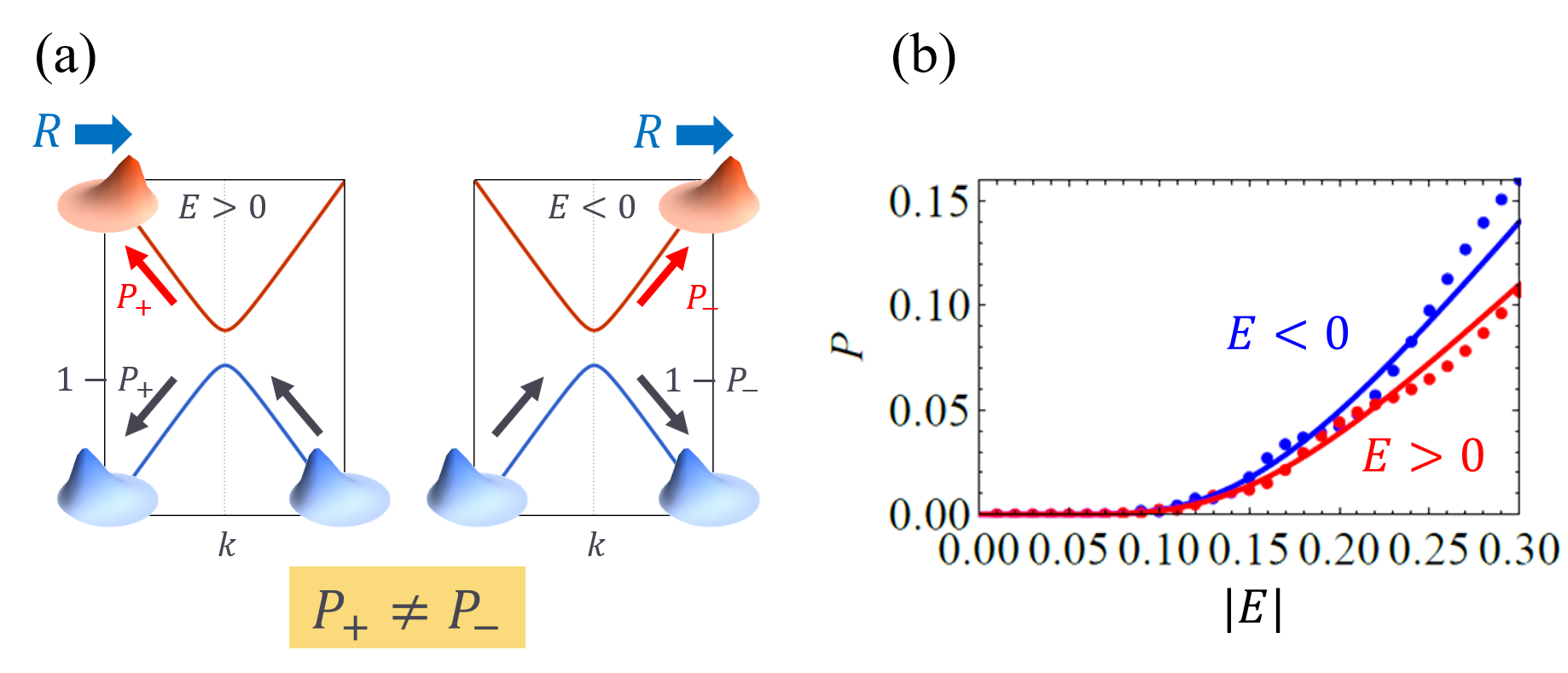
- S. Kitamura, N. Nagaosa, and T. Morimoto: “Nonreciprocal Landau-Zener tunneling”, Commun. Phys. 3, 63 (2020).
トンネリング問題における非平衡定常状態
トンネリング現象における非摂動的なキャリア生成確率の計算については理論手法が確立されており、幅広い研究がなされている一方で、固体中でこのキャリアが運ぶ電流量の理論的な評価は意外にもほとんどなされていません。強い電場によって定常的なキャリア生成が起こっている状況では系が平衡状態から大きくかけ離れてしまい、緩和過程との釣り合いによって生じる非平衡定常状態を決定しなければ系の応答が計算できない困難が背景にはあります。
我々はトンネル確率の複素解析手法と非平衡グリーン関数法を組み合わせて、フェルミオン熱浴中での定常状態を半定量的に計算する公式を導出しました。また、この定常状態では、熱浴への散逸の強さに応じて電流応答が質的に変化することや、空間反転対称性の破れとの協奏により非相反な電流・スピン流が得られうることを示しました。
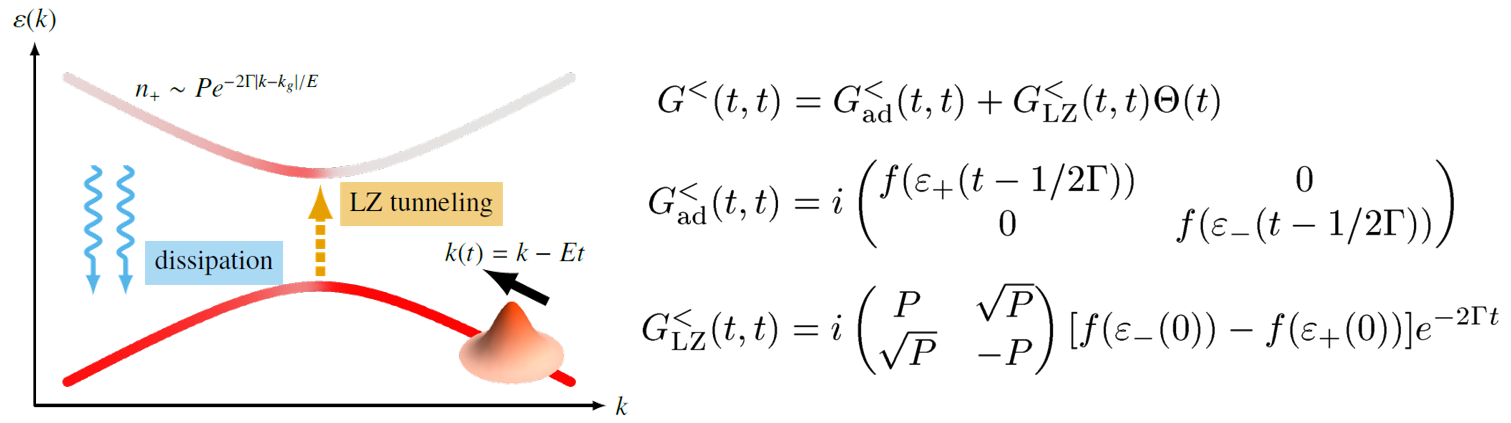
- S. Kitamura, N. Nagaosa, and T. Morimoto: “Current response of nonequilibrium steady states in Landau-Zener problem: Nonequilibrium Green’s function approach”, Phys. Rev. B 102, 245141 (2020).
周期駆動系における新奇量子相の設計・制御
一般に、外場によって駆動された量子系の性質を調べるためには時間依存Schrödinger方程式を直接解く必要があります。しかし系に加わる外場が周期的である場合は、ハミルトニアンが時間に関する離散的な並進対称性を持つため、それに対応する保存量を考えることができます。この保存量は駆動周波数を単位としたエネルギーの小数部分に対応しており、擬エネルギーと呼ばれています。
Floquet理論という微分方程式の理論を応用すると、時間依存Schrödinger方程式をこの擬エネルギーの固有状態を求める問題に帰着させることができます。擬エネルギーのスペクトルを再現する有効ハミルトニアンを考えると、非平衡の問題であるにも関わらず平衡統計力学をベースにした静的な解析によって系の性質が理解できることが多々あります。この有効ハミルトニアンをうまく設計(Floquetエンジニアリング)することで様々な量子状態を実現することを目指した研究をこれまで進めてきました。
レビュー論文・解説
-
T. Oka and S. Kitamura: “Floquet Engineering of Quantum Materials”, Ann. Rev. Cond. Mat. Phys. 10, 387-408 (2019).
-
Takahiro Morimoto, Sota Kitamura, and Naoto Nagaosa:
“Geometric aspects of nonlinear and nonequilibrium phenomena”,
J. Phys. Soc. Jpn. 92, 072001 (2023). -
北村想太: “周期駆動量子系の物理”,
物性若手夏の学校テキスト 1, 81 (2023).
Brillouin-Wignerの摂動論の周期駆動系への応用
Floquet理論を用いた周期駆動量子系の解析にあたっては、系統的に有効ハミルトニアンを構築するフレームワークが不可欠です。有効ハミルトニアンの周波数の逆冪での級数展開はその一つですが、導出方法によって異なる級数が得られることがあります。
これは周期振動する動的な状態を静的な状態にマップする方法が一通りでないことに起因しています。我々はBrillouin-Wignerの摂動論を周期駆動系に応用することで新しいタイプの級数展開を定式化しました。既存手法は動的な状態をユニタリ変換することで有効ハミルトニアンを得る方法になっていますが、この手法では射影を行うことで有効ハミルトニアンが得られます。このような展開手法間の関係も明確にしました。
また、射影の選び方を工夫することで、周波数が低く逆冪展開が破綻する場合にもこのフレームワークが有用であることを、円偏光によって動的に生成されるWeyl点の振る舞いの解析を通じて実証しました。
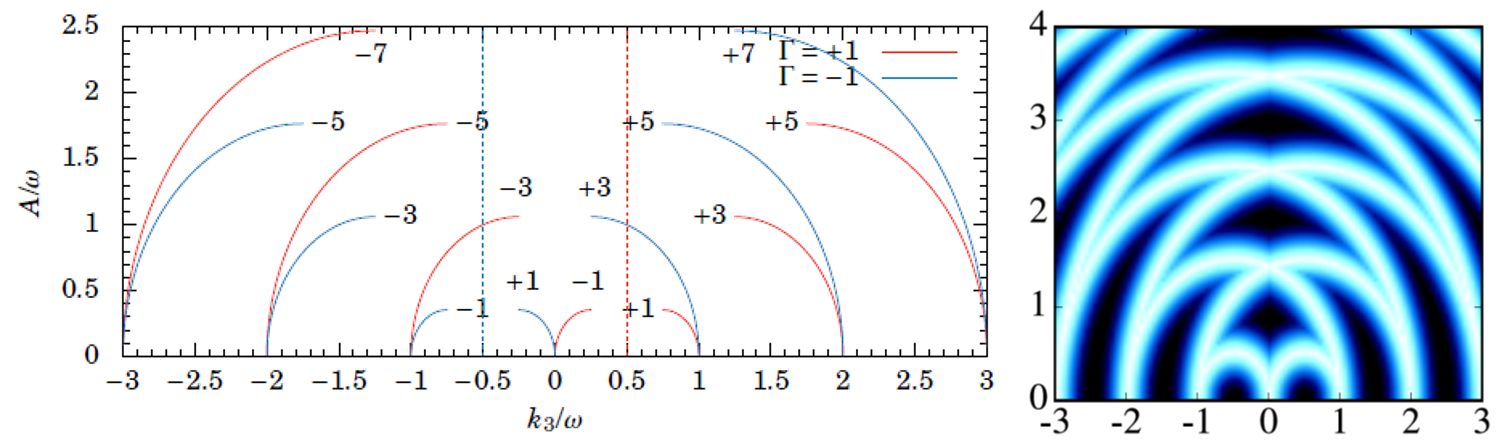
- T. Mikami, S. Kitamura, K. Yasuda, N. Tsuji, T. Oka, and H. Aoki: “Brillouin-Wigner theory for high-frequency expansion in periodically driven systems: Application to Floquet topological insulators”, Phys. Rev. B 93, 144307 (2016).
- L. Bucciantini, S. Roy, S. Kitamura, and T. Oka: “Emergent Weyl nodes and Fermi arcs in a Floquet Weyl semimetal”, Phys. Rev. B 96, 041126(R) (2017).
周期駆動された強結合電子系における新奇量子相
上に述べた周期数の逆冪での展開には量子系の典型的なエネルギーが光子のエネルギーより低いことが必要です。電子間に強い相互作用が働いているモット絶縁体ではこの条件を満たすことは難しく、むしろ応用上は電荷ギャップよりも小さい周波数での駆動に興味がもたれます。
我々は相互作用の逆冪での展開(強結合展開)を周期駆動系に拡張することで、このような状況にも応用できる有効ハミルトニアンの系統的な構築方法を確立しました。この理論を応用するとモット絶縁体のスピン自由度を電場でコントロールすることができます。
また、引力Hubbard模型で強い引力によりBEC型の超伝導状態が実現している状況にもこの理論を応用しました。Hubbard模型はη-SU(2)対称性と呼ばれる隠れた対称性のために引力模型と斥力模型が数学的に等価になることが知られていますが、電場を印加するとこの対称性が破れ、引力系に特有な非平衡現象が現れることを見出しました。
さらに、我々は最近、上記のフレームワークを銅酸化物超伝導体のモデルに適用することで、トポロジカル超伝導が発現する可能性を見出しました。円偏光レーザーで駆動された銅酸化物超伝導体の非平衡状態を超伝導の発現機構まで遡って微視的に記述すると、電子のペアリング相互作用がレーザー電場によって制御でき、高い転移温度に付随して大きなトポロジカルギャップが生じることを示しました。
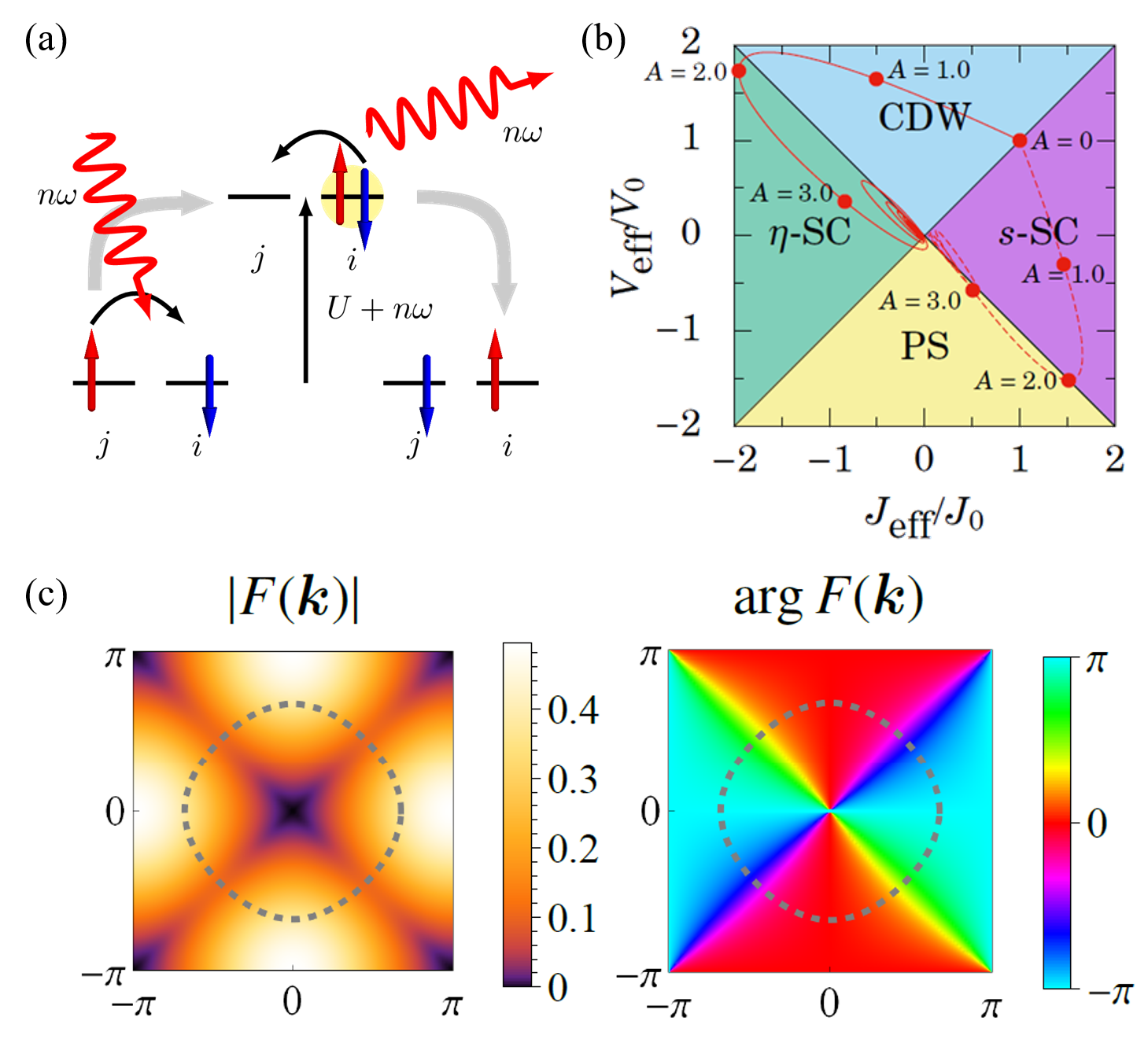
- S. Kitamura, T. Oka, and H. Aoki: “Probing and controlling spin chirality in Mott insulators by circularly polarized laser”, Phys. Rev. B 96, 014406 (2017).
- S. Kitamura and H. Aoki: ”$\eta$-pairing superfluid in periodically-driven fermionic Hubbard model with strong attraction”, Phys. Rev. B 94, 174503 (2016).
- Sota Kitamura and Hideo Aoki:
“Floquet topological superconductivity induced by chiral many-body interaction”,
Commun. Phys. 5, 174 (2022).